Übergangswahrscheinlichkeiten sind eine bestimmte Art von abhängigen/konditionellen Wahrscheinlichkeiten. Der Unterschied zu anderen konditionellen Wahrscheinlichkeiten liegt darin, dass das Ziel und die vorgegebenen Ereignisse zu verschiedenen Zeiten auftreten. Diese zeitliche Verschiebung wird oft als "lag" bezeichnet. Daher wird unsere Sequenzanalyse auch als Lag Sequential Analysis bezeichnet.
Es zeigt Ihnen auf Grundlage der gesammelten Daten, wie wahrscheinlich es ist, dass ein bestimmter Code von einem anderen Code gefolgt wird. Da die Berechnung aber konditionell ist, basiert der Prozentwert auf der Anzahl der entdeckten Sequenzen pro Code (Rohsumme), nicht auf der Gesamtzahl der Ereignisse oder gefundenen Sequenzen.
Diese Übergangswahrscheinlichkeiten werden als einfache deskriptive Statistiken behandelt.
Übergangsergebnisse
Die Übergangswahrscheinlichkeiten in INTERACT basieren auf einer Formel aus dieser Publikation:
Observing interaction: An introduction to sequential analysis
(Second edition)
Roger Bakeman - Georgia State University
John M. Gottman - University of Washington
Cambridge university press
Der Reiter 'Übergangswahrscheinlichkeiten' sieht wie folgt aus:
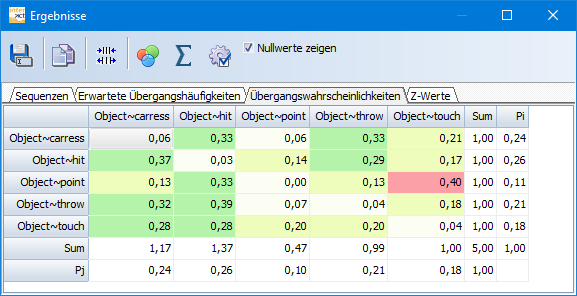
Die sichtbare Anzahl multipliziert mit 100 zeigt Ihnen die Wahrscheinlichkeit in %.
Diese Werte werden auf Grundlage der Häufigkeiten, die im ersten Reiter Sequenzen zu finden sind, berechnet.
Hinweis: Berechnungsdetails sind zu finden unter Übergangsberechung.